|
Beats—What They are and What Causes Them ©Copyright by Robert Chuckrow 2012 Beats occur when two frequencies that differ by less than about 15 Hz are sounded together. Beats are the loudening and softening of the combined sound of the two frequencies. It turns out that the beat rate is found by subtracting the two frequencies. If you click this link, a new window will open. You will hear a 440-Hz tone, then a 442-Hz tone, and finally the combination of those two tones, beating at 2 beats per second. When two frequencies that differ by about 15 Hz are sounded together, beats occur that are very unpleasant. If you click this link, a new window will open. You will hear a 440-Hz tone, then a 455 Hz tone, and finally the combination of those two tones, beating at 15 beats per second. Why the beat rate is the difference between the two frequencies is explained as follows: Imagine the cone of a loud-speaker vibrating at a given frequency. The motion of the cone toward the observer produces a compression of the air, which means that the air near the cone has a pressure higher than atmospheric. This compression moves off at the speed of sound. Similarly, the motion of the cone away from the observer produces a rarefaction of the air, which means that the air near the cone has a pressure lower than atmospheric. This rarefaction also moves off at the speed of sound. When the successive compressions and rarefactions reach the observer’s ear, they cause the ear drum to move inward and outward, respectively. This phenomenon causes a perception of a tone, the pitch of which is related to the frequency of vibration, and the loudness of which is related to the amplitude of the vibration. What happens when two loud-speakers, side by side vibrate at the same frequency? If they are in phase (which means that their cones are both moving in the same direction at each instant of time), their effects add, and a louder sound is heard. This phenomenon is called constructive interference. If they are out of phase, which means that they are moving in opposite directions at each instant of time, their effects tend to cancel, and a softer sound is heard. This phenomenon is called destructive interference. Now, if the two frequencies of the cones are slightly different, they will be alternately in and out of phase. Consequently, beats will be heard. Click here to view and hear two vibrating tuning forks of slightly different frequencies, illuminated by a stroboscope, moving in and out of phase and beating approximately once every three seconds. The beat rate is the mathematical difference between the two frequencies. To see this relationship, suppose that the respective frequencies of the loudspeakers are 400 Hz and 401 Hz. If the cones are moving in phase at a certain instant of time, then, 1 s later they will again be in phase. This concurrence exists when each cone has undergone an integral number of complete vibrations, in this case, 400 and 401, respectively. Now, after 1/2 s, the 400-Hz cone will have undergone 400/2 = 200 complete vibrations, and the 401 Hz cone has undergone 401/2 = 200.5 vibrations. Therefore, they are now 1/2 vibration out of phase. Thus, during each second, the vibrations of the cones are in and then out of phase once. Therefore, 1 beat per second (1 b/s) is heard. Next suppose that the respective frequencies of the cones are 400 Hz and 402 Hz. If they are in phase at a certain instant, then, 1 s later they will again be in phase. Here the cones have undergone 400 and 402 complete vibrations, respectively. Moreover, after 1/2 s, they are also in phase, having undergone 200 and 201 complete vibrations respectively. However, after 1/4 s they are 1/2 vibration out of phase, having undergone 100 and 100.5 vibrations, respectively. Thus, we hear 2 b/s. In general, it can be seen that two frequencies of f and f + n will produce n beats/s. Thus the beat frequency is fb = |f2 – f1| (the beat frequency must be positive, hence the absolute value is used). Click here for a video explaining beats and showing them visually. In the sketch below, the width of the graph paper corresponds to one second. Two sine waves are drawn, one above the other. The top sine wave undergoes four complete vibrations and, thefore, has a frequency of 4 Hz. Similarly, the lower sine wave has a frequency of 5 Hz. The lowermost waveform is the addition of the 4- and 5-Hz sine waves. That is, the displacement of the lowermost waveform at any time is the sum of the displacements of the two waveforms above it. The resultant waveform is seen to beat at 1 Hz, the difference of the two component frequencies: 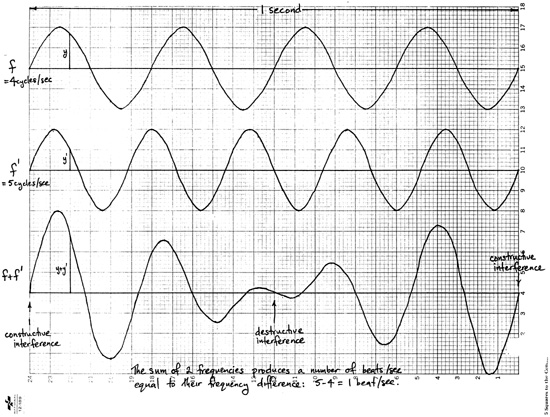 Note: In the above figure, it can be seen that the period of the beat sum of the 4- and 5-Hz sine waves is intermediate between that of the two components (look at the leftmost period of each waveform). This relationship implies that the frequency of the combined tone is less than that of the higher tone and greater than that of the lower tone. This effect is demonstrated in the following sound file (click this link). First a 250-Hz tone is sounded, then a 240-Hz tone is sounded, and then these tones are combined, producing 10 beats/second. Next, the combined tone is sounded, immediately followed by a 250-Hz tone. The combined tone is easily perceived to be lower in pitch than the 250-Hz tone. Finally, the combined tone is sounded, immediately followed by a 240-Hz tone. The combined tone is easily perceived to be higher in pitch than the 240-Hz tone. Watch a nicely done video on beats on youtube.com. ©Copyright 2011 by Robert Chuckrow |
